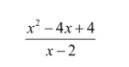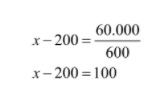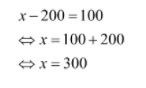Hallo Sahabat TutorIndonesia!
Sifat – sifat pada Operasi Aljabar merupakan salah satu konsep matematika yang paling penting dan perlu dipelajari, bahkan pada tingkat menengah. Aljabar memakai huruf atau simbol untuk mewakili angka dan melakukan berbagai operasi matematika.
aljarbar memiliki beberapa sifat-sifat dasar dan operasi aljabar yang mendasarinya. Artikel ini akan menjelaskan sifat-sifat aljabar dan beberapa operasi aljabar yang biasa digunakan pada tingkat menengah.
baca juga : guru les privat
Mengenal apa itu aljabar?

Aljabar adalah cabang matematika yang memungkinkan kita untuk mengungkapkan hubungan matematika dengan cara yang lebih umum dan abstrak. Aljabar menggunakan huruf dan variabel untuk mewakili angka dan kuantitas yang tidak diketahui. Ini akan membantu Anda memecahkan masalah yang lebih kompleks dan mengenali pola dalam masalah matematika.Rumus Aljabar
baca juga : les privat jakarta
ada beberapa rumus yang sering digunakan dalam operasi hitung aljabar. Berikut rumus-rumusnya.
- (a + b)2= a2 + 2ab + b2
- (a – b)2= a2 – 2ab + b2
- (a + b)(a – b) = a2– b2
- (a + b + c)2 = a2+ b2 + c2 + 2ab + 2bc + 2ca
- (a + b)3= a3 + 3a2b + 3ab2 + b3
- (a – b)3= a3 – 3a2b + 3ab2 – b3
PECAHAN DALAM BENTUK ALJABAR

1. Penjumlahan & Pengurangan Pecahan dalam Bentuk Aljabar
Pada prinsipnya sama, untuk menjumlahkan dan mengurangi pecahan bentuk aljabar yakni sama dengan menjumlahkan dan mengurangkan pada pecahan biasa. kamu hanya perlu menyamakan penyebutnya terlebih dahulu. Silahkan sobat perhatikan contoh berikut:

untuk pengurangan simak contoh berikut:
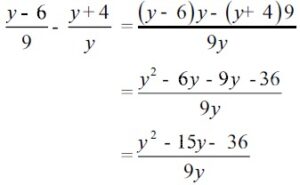
2. Perkalian dan Pembagian Bentuk Aljabar
Perkalian
untuk perkalian tidak jauh berbeda dengan perkalian pecahan. Pembilang kali pembilang, penyebut kali penyebut. selanjutnya, sederhanakan jika ada yang bisa disederhanakan. Rumusnya:

Contoh
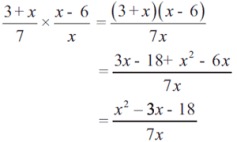
2.Pembagian
untuk pembagian pada bentuk aljabar memiliki kesamaan dengan pembagian pecahan. kamu bisa mengubahnya terlebih dahulu dalam bentuk perkalian yakni dengan membalik pecahan aljbar pembagi. Rumusnya:
![]()
contoh soal:
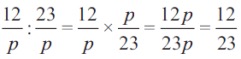
3. Penyederhanaan Pecahan bentuk Aljabar
agar kamu bisa menyederhanakan pecahan aljabar, saat ada faktor persekutuan yang sama antara pembilang dan penyebut. maka kamu perlu menyederhanakannya dahulu. Faktor persekutuan bisa berupa angka atau variabel dengan jenis dan pangkat yang sama. Simak contoh berikut:
Sederhanakan pecahan
10p/24pr
Dari pecahan di atas, terdapat faktor persekutuan yang sama antara pembilang dan penyebut yaitu 2p. Faktor persekutuan ini kita coret sehingga menjadi:
10p/24pr = 2p . 5 / 2p . 12 r = 5/12r
pada beberapa kasus soal, umumnya penyederhanaan pecahan dilakukan dengan memfaktorkan terlebih dahulu. Berikut contohnya
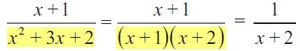
Sifat-sifat Aljabar

Kamu akan menemui beberapa sifat dasar aljabar yang pelu kamu pahami dengan baik. Sifat-sifat itu akan membantumu dalam menyederhanakan ekspresi aljabar dan mempermudah penyelesaian masalah. Berikut adalah beberapa sifat-sifat aljabar yang penting untuk dipahami:
1. Sifat komutatif
Sifat komutatif berlaku pada penjumlahan dan perkalian, yaitu sebagai berikut.
x + y = y + x
xy = yx
2. Sifat asosiatif
Sifat asosiatif berlaku pada penjumlahan dan perkalian, yaitu sebagai berikut.
(x + y) + z = x + (y + z)
(xy)z = x(yz)
3. Sifat distributif
Sifat distributif adalah sifat yang meliputi operasi perkalian menjadi penjumlahan atau pengurangan.
x(b – c) = xb – xc
y(2x + a) = 2xy + ay
4. Pemfaktoran Aljabar
Pemfaktoran aljabar adalah strategi untuk menguraikan persamaan aljabar ke bentuk faktorisasinya. Contohnya adalah sebagai berikut.
x2 – 5x + 6 = 0
Jika difaktorkan, persamaan di atas aan menjadi seperti berikut.
x2 – 5x + 6
x2 + (-3-2)x + (-3 × -2)
Jadi, hasil pemfaktorannya adalah (x – 3)(x – 2).
baca juga : les privat
Contoh soal

Sederhanakan bentuk (3m2– 4m + 5) – (-m2 + 3m – 4)!
Pembahasan:
Pertama, kamu harus mengelompokkan suku-suku yang terdapat variabel sejenis.
(3m2 – 4m + 5) – (-m2 + 3m – 4) = 3m2 – 4m + 5 + m2 – 3m + 4
= 3m2 + m2 – 4m – 3m + 5 + 4
= 4m2 – 7m + 9
Jadi, bentuk sederhana dari (3m2 – 4m + 5) – (-m2 + 3m – 4) adalah 4m2 – 7m + 9.
2. Tulislah kalimat berikut dalam bentuk aljabar!
a. 5000 lebihnya uang Abi sama dengan uang Adi.
b. Jika suatu bilangan dikalikan 5 lalu dikurangi enam, akan menghasilkan bilangan 14.
c. Yofa membeli 5 buah pensil dan 2 buah pulpen dengan harga Rp4.000.
Pembahasan:
a. Rp5.000 lebihnya uang Abi sama dengan uang Adi.
Misalkan, uang Adi dinyatakan sebagai x dan uang Abi sebagai y.
Kalimat di atas menjadi: x = y + 5.000
b. Misalkan, bilangan yang dimaksud dinyatakan sebagai m, sehingga kalimat aljabarnya menjadi seperti berikut.
(m × 5) – 6 = 14
5m – 6 = 14
c. Misalkan, pensil dinyatakan sebagai pdan pulpen sebagai q, maka kalimat aljabarnya menjadi seperti berikut.
5p + 2q = 4.000
Tentukan hasil pembagian antara

Pembahasan:
Pertama, kamu harus memfaktorkan pembilangnya. Jika difaktorkan, menjadi seperti berikut.
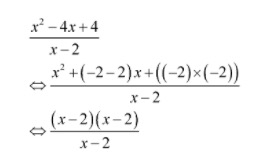
Selanjutnya, lakukan pembagian antara hasil pemfaktoran dan penyebutnya.
- Pedagang Bakso aci membeli 10 kg tepung aci seharga Rp60.000. Dari 10 kg tepung aci, si pedagang bisa membuat 600 buah Bakso aci. Pedagang tersebut ingin mendapatkan untung Rp200 dari satu Bakso aci buatannya. Kira-kira, berapa harga jual Bakso acinya?
Solusi:
- Pertama, kamu harus memisalkan harga jual bakso acinya sebagai x. Hal itu karena harga jual bakso aci merupakan variabel yang bisa berubah akibat harga beli tepung acinya.
- Kedua, carilah harga baksoaci sebelum ditambah untung Rp200. Secara matematis, ditulis sebagai x– 200.

Harga jual bakso aci sebelum ditambah untung Rp200 adalah Rp100.
- Ketiga, tentukan harga jual bakso aci agar keuntungannya Rp200.

Jadi, agar pedagang mendapatkan untung Rp200, ia harus menjual bakso acinya Rp300/biji.
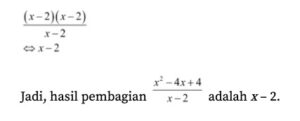
Jadi, apa lagi yang ditunggu? Hubungi kami segera di line telepon (021) 77844897 atau kamu juga bisa menghubungi kami via 087781609961. Atau klik www.tutorindonesia.co.id untuk mendapatkan informasi lebih lanjut.
Sampai ketemu di TutorIndonesia
Referensi :
- latisprivat.com
- grid.id