Halo sahabat tutorindonesia!

Polinomial adalah salah satu konsep dasar dalam aljabar yang sering digunakan dalam berbagai cabang matematika dan ilmu terapan. Memahami syarat-syarat polinomial sangat penting, baik dalam konteks teori matematika murni maupun dalam aplikasinya. Artikel ini akan membahas syarat polinomial secara rinci, termasuk syarat, sifat, dan aplikasinya.

Definisi Polinomial

harga guru private ke rumah, les privat bekasi, jasa les privat, biaya les sd per bulan, biaya les privat sd, biaya les privat per bulan, biaya les privat jakarta, biaya les privat per hari, biaya les privat, harga les privat, biaya les rumahan, biaya les privat untuk anak tk, Les Privat TK, guru privat bahasa inggris, tutor privat

Sumber: Freepik

Polinomial adalah ekspresi matematika yang terdiri dari variabel, koefisien, dan operasi penjumlahan, pengurangan, serta perkalian dengan peringkat non-negatif dari variabel. Sistem persamaan polinomial (suku banyak) adalah sistem persamaan dengan pangkat tertingginya lebih besar dari 2 ( > 2). Bentuk umum dari polinomial adalah sebagai berikut:

Dimana :

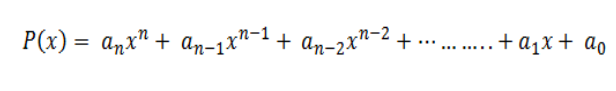
Derajat (n) adalah pangkat tertinggi dalam suatu suku banyak.
Variabel (x) adalah bilangan yang dimisalkan dengan huruf misalnya x.
Koefisien (a) adalah bilangan yang mengikuti variabel.

Syarat Polinomial

Untuk suatu ekspresi matematika dikatakan polinomial, harus memenuhi syarat-syarat berikut:

1. Variabel dengan Pangkat Non-Negatif

Variabel dalam polinomial hanya boleh berada dalam bentuk pangkat non-negatif (0, 1, 2, dst.). Pangkat negatif atau fraksional tidak diperbolehkan.

2. Koefisien Terbatas

Koefisien dari variabel-variabel dalam polinomial adalah bilangan real (atau bilangan kompleks), dan harus terbatas, yaitu tidak ada pembagian atau akar yang melibatkan variabel.
Penjumlahan dan Pengurangan Terbatas: Polinomial hanya dapat menggunakan operasi penjumlahan dan pengurangan antar monom.

Sifat Polinomial

Sumber: Freepik

Beberapa sifat penting dari polinomial meliputi:
a. Derajat Polinomial
Derajat polinomial adalah peringkat tertinggi dari variabel dengan koefisien bukan nol. Misalnya, pada polinomial 4×3−3×2+2x−1, derajatnya adalah 3.

B. Koefisien Polinomial
Koefisien adalah bilangan yang mengalikan setiap monom dalam polinomial. Dalam polinomial 2×3−5x+7 koefisiennya adalah 2 untuk x3, -5 untuk x, dan 7 untuk konstanta.

C. Term dan Monom
Polinomial terdiri dari satu atau lebih istilah, yang dikenal sebagai monom. Setiap monom adalah produk dari koefisien dan variabel yang diangkat. Contoh polinomial 3×4−2×3+x−6 memiliki empat monom: 3x43x^43×4, −2×3-2x^3−2×3, x, dan −6.

D. Polinomial Khusus
Polinomial Konstanta: Polinomial dengan derajat 0, contohnya P(x)=5
Polinomial Linear: Polinomial dengan derajat 1, contohnya P(x)=2x+3.
Polinomial Kuadrat: Polinomial dengan derajat 2, contohnya P(x)=x2−4x+4.

Fungsi Polinomial
Polinomial dapat digunakan untuk mendefinisikan fungsi polinomial f(x)=P(x)f(x) = P(x)f(x)=P(x). Fungsi polinomial bersifat kontinu dan terdiferensiasi di seluruh domainnya.

1. Polinomial Panjang dan Reduksi
Polinomial dapat direduksi atau direduksi dengan menggabungkan term-term yang serupa. Misalnya, polinomial 2×2+3x−x2+5 dapat direduksi menjadi x2+3x+5

2. Operasi pada Polinomial
Polinomial dapat dijumlahkan, dikurangkan, atau dikalikan. Namun, pembagian polinomial biasanya melibatkan algoritma pembagian polinomial, dan hasilnya bisa berupa polinomial dengan sisa.

Jenis Fungsi Polinomial dan Karakteristiknya

Sumber: Freepik

Fungsi polinomial adalah salah satu konsep dasar dalam matematika, khususnya dalam aljabar. Fungsi ini memiliki bentuk umum yang melibatkan penjumlahan beberapa suku, di mana setiap suku adalah hasil perkalian koefisien dengan variabel yang dipangkatkan dengan bilangan bulat non-negatif. Berikut adalah berbagai jenis fungsi polinomial dan karakteristik utamanya:

1. Fungsi Polinomial Linear
Fungsi polinomial linear adalah fungsi polinomial dengan derajat 1. Bentuk umumnya adalah:
f(x)=ax+b
di mana aaa dan bbb adalah konstanta, dan a≠0a \neq 0a=0. Fungsi ini menghasilkan grafik berupa garis lurus dengan kemiringan yang ditentukan oleh aaa dan intersep pada sumbu yyy yang ditentukan oleh bbb.
Contoh: f(x)=3x+2
Karakteristik:

Derajat: 1
Bentuk grafik: Garis lurus
Kemiringan: a
Intersep y: b

2. Fungsi Polinomial Kuadrat
Fungsi polinomial kuadrat adalah fungsi polinomial dengan derajat 2. Bentuk umumnya adalah:

f(x)=ax2+bx+c
di mana a, b, dan c adalah konstanta, dengan a≠0. Grafik dari fungsi ini berbentuk parabola.
Contoh: f(x)=2×2−3x+1

Karakteristik:
Derajat: 2
Bentuk grafik: Parabola
Arah parabola: Terbuka ke atas jika a>0 dan terbuka ke bawah jika a<0 Titik balik (vertex): Titik terendah atau tertinggi dari parabola

3. Fungsi Polinomial Kubik
Fungsi polinomial kubik adalah fungsi polinomial dengan derajat 3. Bentuk umumnya adalah:
f(x)=ax3+bx2+cx+d
di mana aaa, bbb, ccc, dan ddd adalah konstanta, dengan a≠0. Grafik fungsi ini dapat memiliki bentuk yang lebih kompleks, termasuk perubahan arah yang lebih banyak dibandingkan dengan fungsi kuadrat.
Contoh: f(x)=x3−6×2+11x−6

Karakteristik:

Derajat: 3
Bentuk grafik: Kurva dengan kemungkinan satu atau dua titik belok
Perubahan arah: Dapat memiliki hingga dua titik belok

4. Fungsi Polinomial Kuadrat Lebih Tinggi
Fungsi polinomial dengan derajat lebih tinggi dari 3 termasuk fungsi kuadrat yang lebih kompleks seperti derajat 4, 5, dan seterusnya. Bentuk umumnya adalah:
f(x)=anxn+an−1xn−1+…+a1x+a0

di mana n adalah derajat polinomial dan an≠0

Contoh: f(x)=x4−4×3+6×2−4x+1

Karakteristik:
Derajat: Lebih dari 3
Bentuk grafik: Dapat memiliki beberapa titik belok, lebih kompleks
Perilaku: Bergantung pada derajat dan koefisien polinomial

Fungsi polinomial mencakup berbagai jenis fungsi berdasarkan derajatnya, mulai dari fungsi linier yang sederhana hingga polinomial dengan derajat tinggi yang kompleks. Memahami karakteristik setiap jenis fungsi polinomial sangat penting dalam berbagai aplikasi matematika, mulai dari pemodelan data hingga analisis grafik. Dengan mengetahui bentuk grafik dan sifat-sifat fungsi ini, kita dapat lebih baik dalam menyelesaikan masalah dan memahami fenomena matematika yang lebih luas.

Bagaimana Mengidentifikasi Fungsi Polinomial?
Fungsi polinomial adalah salah satu jenis fungsi matematika yang sangat penting dan sering ditemukan dalam berbagai konteks, mulai dari aljabar hingga kalkulus. Mengidentifikasi fungsi polinomial adalah keterampilan dasar yang penting untuk memahami bagaimana fungsi ini berperilaku dan bagaimana mereka dapat digunakan dalam berbagai aplikasi. Simak cara mengidentifikasi fungsi polinomial dengan langkah-langkah yang jelas dan contoh yang relevan:

Langkah-langkah Mengidentifikasi Fungsi Polinomial
1. Periksa Bentuk Umum
Fungsi polinomial harus mengikuti bentuk umum:

f(x)=anxn+an−1xn−1+⋯+a1x+a0

Periksa apakah fungsi yang diberikan sesuai dengan bentuk ini. Jika fungsi dapat diubah menjadi bentuk ini, maka itu adalah fungsi polinomial.

Contoh:

Fungsi f(x)=3×4−5×2+2 adalah fungsi polinomial dengan derajat 4.
Fungsi g(x)=1x+2 bukan fungsi polinomial karena terdapat pembagian dengan xxx, bukan hanya penjumlahan dan perkalian.

2. Cek Koefisien dan Derajat
Fungsi polinomial harus memiliki koefisien tetap dan derajat yang merupakan bilangan bulat non-negatif. Derajat polinomial adalah pangkat tertinggi dari x dalam fungsi tersebut.

Contoh:

Fungsi h(x)=−2×3+4x−7 memiliki derajat 3.
Fungsi k(x)=3ex+5 bukan fungsi polinomial karena terdapat eksponensial ex yang tidak sesuai dengan bentuk polinomial.

3. Periksa Apakah Fungsi Memiliki Pecahan atau Akar yang Melibatkan Variabel

Fungsi polinomial tidak boleh memiliki pecahan yang melibatkan variabel x di penyebut atau akar yang melibatkan variabel x. Semua eksponen variabel x harus berupa bilangan bulat non-negatif.

Contoh:

Fungsi m(x)=x1/2+3 bukan fungsi polinomial karena eksponen 1/2 bukan bilangan bulat.
Fungsi n(x)=2×2+1 bukan fungsi polinomial karena ada pecahan dengan x di penyebut.

4. Periksa Penambahan, Pengurangan, dan Perkalian
Fungsi polinomial dapat melibatkan penambahan, pengurangan, dan perkalian koefisien serta variabel, tetapi tidak melibatkan operasi yang menghasilkan eksponen bukan bilangan bulat atau variabel dalam penyebut.

Contoh:

Fungsi p(x)=6×2−4x+5 adalah fungsi polinomial.
Fungsi q(x)=(x+1)2 juga merupakan fungsi polinomial karena setelah diekspansi menjadi x2+2x+1.

Jadi, apa lagi yang ditunggu? Hubungi kami segera di saluran telepon (021) 77844897 atau Anda juga dapat menghubungi kami melalui 085810779967 . Atau klik www.tutorindonesia.co.id untuk mendapatkan informasi lebih lanjut.