Hai sahabat TutorIndonesia, apa kabar kalian? Sudah siap belajar pekan ini? Mari kita lanjutkan ilmu matematika yang masih berkaitan dengan titik dan garis. Apa itu? Dia adalah persamaan garis lurus. Kalian pasti pernah menggaris kan? Biar tidak bingung dengan istilah persamaan, maka ayo kita coba cerna satu per satu.
Pengertian Persamaan Garis Lurus
Kalian sudah biasa membuat garis dengan penggaris tapi maksud dari garis lurus bukanlah garis lurus dari penggaris. Jadi Garis lurus merupakan garis dengan kemiringan yang stagnan atau sama pada setiap ruasnya. Nah kata kuncinya adalah kemiringan. Lho katanya garis lurus, kok malah miring?
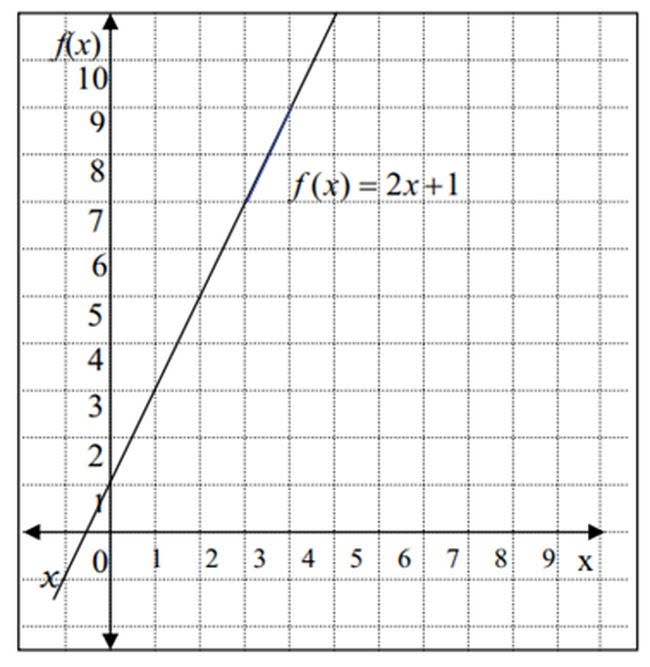
Nah, kalian bisa melihat gambar tersebut ya! Persamaan garis lurus memiliki perbandingan yang sama. Artinya antara selisih koordinat y dan selisih koordinat x bernilai serupa. Maka, persamaan garis lurus adalah perbandingan selisih koordinat y dan selisih koordinat x. Jadi garis itulah yang akan kita bahas.
Pada grafik di atas diketahui fungsi f(x) = 2x + 1. Sumbu mendatar disebut sumbu x dan sumbu tegak disebut sumbu f(x). Jika fungsi di atas dituliskan dalam bentuk y = 2x + 1, maka sumbu tegak disebut sumbu y. Jadi, y = f(x).
Kalau kalian sedikit bingung dengan sumbu x dan y, kalian bisa tengok-tengok kembali blog-blog sebelumnya ya.
Sifat Persamaan Garis Lurus
Ada empat sifat yang dimiliki dari persamaan ini. Mereka adalah:
1. Garis Sejajar
2. Garis Berimpit
3. Garis Tegak Lurus
4. Garis Berpotongan
Apakah sifat-sifat itu berbeda banget? Kalian baru dapat melihatnya lebih jelas jika sudah mengaplikasikannya ke dalam diagram Kartesius.
Rumus
Berhubung persamaan ini memiliki dua bentuk yaitu eksplisit dan implisit, maka kita juga perlu mencari tau pengertian keduanya ya.
Bentuk Eksplisit adalah bentuk persamaan garis lurus dituliskan dengan y = mx + c dimana x dan y merupakan variabel sedangkan m dan c adalah konstanta. Dalam hal ini, m sering disebut koefisien arah atau gradien dari garis lurus. Sehingga untuk garis yang persamaannya y = 2x + 1 dengan gradien m = 2.
intinya gradien atau kemiringan garis merupakan besarnya perbedaan tinggi (y) dibanding besarnya perbedaan datar (x). Sehingga, gradien suatu garis bisa didefinisikan sebagai berikut:
rumus gradien garis
Bentuk implisit dimana persamaan y = 2x + 1 dapat diubah ke bentuk lain yaitu 2 x – y + 1 = 0. Jadi, bentuk umum lain dari persamaan garis lurus dituliskan dengan Ax + By + C = 0
Gradien suatu garis juga bisa bernilai positif atau negatif. Apabila garisnya naik dari kiri ke kanan maka gradiennya positif. Sebaliknya, kalau garisnya turun dari kiri ke kanan maka gradiennya negatif.
Sudah pusing? Mimin juga sedikit migrain nih.
untuk mencari persamaan garis lurus sendiri terdapat dua cara. Pertama jika gradiennya diketahui dan garis melalui satu titik, kedua jika diketahui dua titik yang dilalui garis. Berikut rumus persamaan garis lurus:
– Diketahui gradien dan satu titik yang dilalui garis, maka y – y1 = m (x-x1)
– rumus kedua akan mimin bagikan lewat gambar.
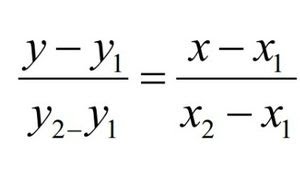
Agak ribet sih kelihatannya ya kan? Maka dari itu memang sebaiknya langsung ke soal saja. Gimana? Sudah siap belum? Karena memang nih ya tidak terlalu banyak teori dari ini.
Cara Menggambar
Gambarlah grafik dari persamaan garis lurus y = 3x – 9!
1. Cari titik potong di sumbu x
Cara mencari titik potong pada sumbu-x adalah dengan membuat variabel y menjadi 0.
Jadi, saat y = 0, nilai x yang dihasilkan adalah 3. Sehingga, diperoleh titik potong di sumbu-x adalah (3,0).
2. Cari titik potong di sumbu y
Tidak jauh berbeda dengan cara mencari titik potong pada sumbu-x, untuk mencari titik potong di sumbu-y, kita harus mengganti variabel x menjadi 0.
Jadi, saat x = 0, nilai y yang dihasilkan adalah -9. Sehingga, diperoleh titik potong di sumbu-y adalah (0,-9).
3. Gambar garis yang menghubungkan titik potong tersebut
Setelah diperoleh dua buah titik potongnya, kita bisa tarik garis lurus yang menghubungkan kedua titik potong tersebut.
Baiknya kalian langsung coba deh ya!
Contoh Soal
1. Carilah persamaan garis lurus yang melalui titik P (1,1) dan Q (2,2)
Jawab.
Mari masukkan ke rumus kedua karena kita memiliki dua X dan dua Y.
Y – 1/2-1 = X – 1/2-1
Y-1/1 = X -1/1
= (Y-1)1 =(x-1)1
Y-1-x-1
Y-x-2 = 0
X-y-2 = 0
Gimana sahabat Latis?
2. Tentukan gradien dari x-y-2 = 0
Jawab:
Jangan lupa jika gradien adalah m yang mana bisa kita dapatkan setelah menjabarkan rumus y= mx +c.
Maka -y = m(-x)+2
m = ?
Coba kalian hitung ya berapakah m. Itung-itung kalian bantu mimin nih.
3. Tentukan persamaan garis lurus jika diketahui informasi berikut ini:
Memiliki gradien = 3
Melalui titik (2, 1)
Jawab:
menggunakan rumus persamaan garis lurus seperti di bawah ini.
y – 1 = 3(x – 2)
y = 3x – 6 + 1
y= 3x – 5
Ini kan udah tiga contoh soal nih, kira-kira kalian udah bisa mencernanya belum? Mimin udah kehabisan ide nih mau ngasi soal apalagi, yang jelas mimin capek sih ngetiknya, hahaha.
Setelah mendapat pencerahan dari beberapa penjelasan di atas kira-kira gimana nih Sahabat Tutorindonesia? pembahasan materi persamaan garis lurus susah ga sih? Biar makin paham materinya yuk ikutan les di tutorindonesia.co.id dijamin nilai kamu bakal meningkat drastis.
Baca juga: Les Privat SBMPTN
Referensi:
1. detik.edu
2. ruangguru.com
